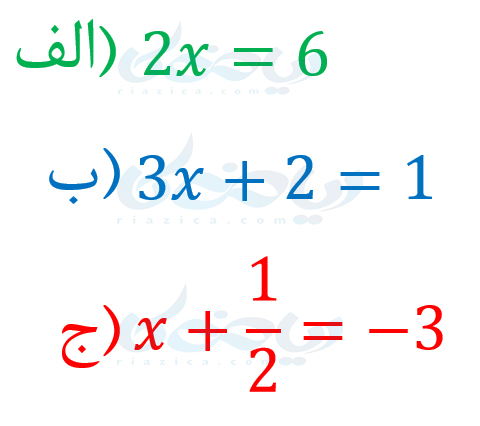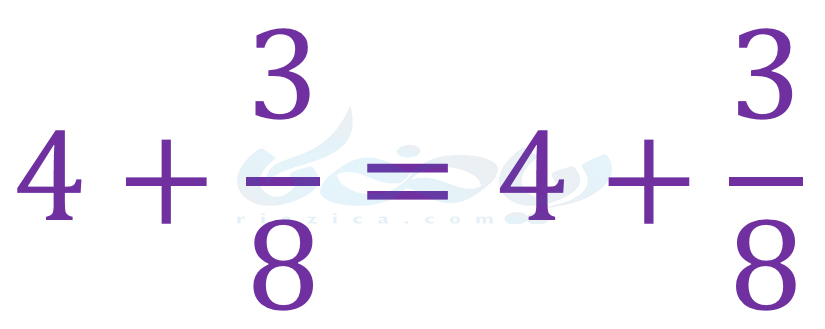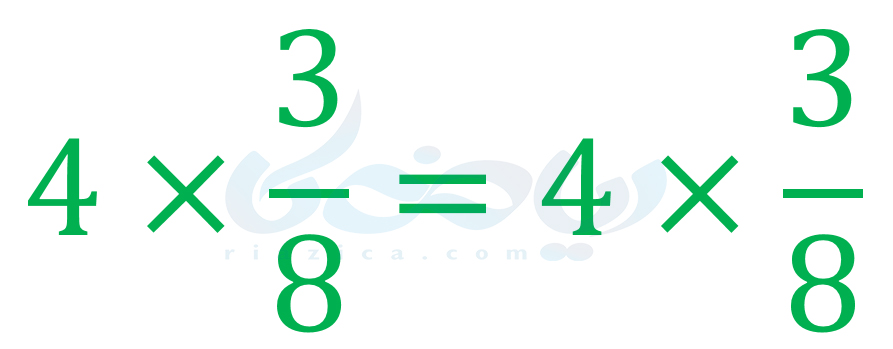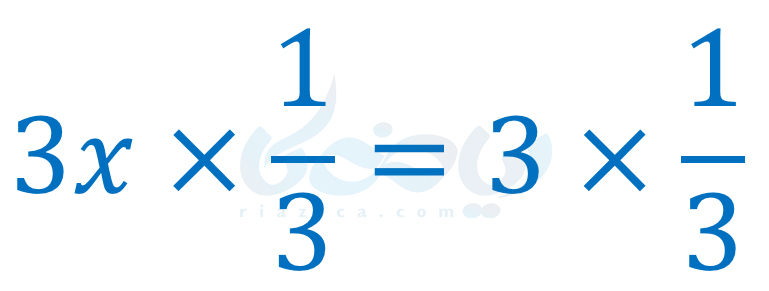در جدیدترین مطلب آموزشی سایت زنگ تفریح به این میپردازیم که معادله چیست؟ و چه ویژگی هایی دارد. در ادامه ما را همراهی کنید تا این مبحث دشوار را به ساده ترین شکل بیاموزید.
معادله چیست
آموزش آسان با تمرین
به یک تساوی که دو طرف آن، عبارتهای جبری باشد، معادله میگویند. مثلاً هر یک از عبارتهای زیر، معادله هستند:
همانطور که در درسنامۀ مقدار عددی یک عبارت جبری گفتیم، میتوان به جای متغیرهای عبارتهای جبری، اعداد را جا گذاری کرد. برای معادلات نیز میتوانیم این کار را به یک شرط انجام دهیم. شرط ما بر قرار ماندن تساوی است. مثلاً معادلۀ “الف” را که در بالا نوشتیم در نظر بگیرید. اگر به جای x، عدد 3 را قرار دهیم، داریم:
2×3=6
همانطور که میبینید تساوی عددی برقرار است. اما اگر به جای x، عدد 4 را قرار دهیم، داریم:
2×4≠6
به عبارت دیگر، حاصل 2×4 برابر با 8 میشود، نه 6. بنابراین تساوی عددی برقرار نیست. اصطلاحاً میگوییم 3 پاسخ معادلۀ 2×3=6 است. روش به دست آورن پاسخ یک معادله را حل آن معادله میگوییم. در قسمت بعدی از درسنامۀ معادله ریاضی هفتم به روش حل معادله میپردازیم.
روش حل معادله ریاضی هفتم
میتوانیم پاسخ یک معادله را با سعی و خطا به دست آوریم. مثلاً معادلۀ 2x+1=7 را در نظر بگیرید. اگر از یک شروع کرده و اعداد طبیعی را امتحان کنیم، خواهیم دید که عدد 3 پاسخ این معادله است. اما این روش اصلاً مناسب نیست. اولاً لزوماً پاسخ یک معادله، عدد طبیعی یا صحیح نیست. ثانیاً هیچ تضمینی وجود ندارد که در تلاشهای اولیه به جواب برسیم. همۀ اینها به کنار، در آینده با معادلاتی روبه رو میشویم که حتی در اعداد حقیقی پاسخی ندارند. بنابراین به دنبال روشی هستیم که با طی کردن تعدادی گام مشخص (نه با سعی و خطا) به پاسخ برسیم. در قسمت بعدی از درسنامۀ معادله ریاضی هفتم ابتدا یک مطلب مهم را در مورد تساویها توضیح داده و سپس روش حل معادله را بیان میکنیم.
جمع دو طرف تساوی با یک عدد
اگر دو طرف یک تساوی را با یک عدد جمع کنیم، چه اتفاقی میافتد؟ آیا باز هم تساوی برقرار است؟ مثلاً تساوی زیر را در نظر بگیرید:
اگر دو طرف تساوی را با یک عدد صحیح مثبت مثل 3 جمع کنیم، آنگاه خواهیم داشت:
تساوی بالا درست است. زیرا 4+3 در دو طرف تساوی برابر با 7 میشود. اگر دو طرف تساوی را با یک عدد صحیح منفی مثل −5 جمع کنیم چه طور؟ باز هم تساوی برقرار است؟ این کار را انجام میدهیم:
باز هم تساوی برقرار است. زیرا دو طرف تساوی برابر با −1 میشود. جمع کردن با اعداد گویا و یا به طور کلی اعداد حقیقی نیز، اشکالی ایجاد نمیکند. مثلاً میتوانیم دو طرف تساوی را با عدد 38 جمع کنیم:
تساوی برقرار است چون دو طرف آن برابر با 358 است. حتی ضرب دو طرف تساوی در یک عدد حقیقی نیز مشکلی به وجود نمیآورد. در قسمت بعدی از درسنامۀ معادله ریاضی هفتم به این موضوع میپردازیم.
ضرب دو طرف تساوی در یک عدد
همۀ کارهایی که در قسمت قبل برای جمع انجام دادیم، برای ضرب نیز میتوانیم انجام دهیم. مثل قبل، تساوی 4=4 را در نظر بگیرید. اگر دو طرف تساوی را در یک عدد صحیح مثبت مثل 3 ضرب کنیم، آنگاه خواهیم داشت:
تساوی بالا درست است. زیرا 4×3 در دو طرف تساوی برابر با 12 میشود. اگر دو طرف تساوی را در یک عدد صحیح منفی مثل −5 ضرب کنیم چه طور؟ باز هم تساوی برقرار است؟ این کار را انجام میدهیم:
باز هم تساوی برقرار است. زیرا دو طرف تساوی برابر با −20 میشود. ضرب کردن در اعداد گویا و یا به طور کلی اعداد حقیقی نیز، اشکالی ایجاد نمیکند. مثلاً میتوانیم دو طرف تساوی را در عدد 38 ضرب کنیم:
تساوی برقرار است چون دو طرف آن برابر با 32 است. بنابراین میتوانیم دو طرف یک تساوی را با یک عدد حقیقی جمع و یا در یک عدد حقیقی ضرب کنیم. با توجه به این مطلب، در قسمت بعدی از درسنامۀ معادله ریاضی هفتم، به روش حل معادله میپردازیم.
حل معادله
فرض کنید معادلۀ زیر را به ما داده و از ما خواستهاند که پاسخ معادله را پیدا کنیم.
همانطور که گفتیم باید سعی کنیم معادله را طوری ساده کنیم تا یک طرف تساوی عدد باقی بماند و یک طرف دیگر متغیر. بنابراین سعی میکنیم کاری کنیم تا در سمت راست تساوی بالا عدد باقی بماند و در سمت چپ متغیر (البته میتوانستیم این کار را به صورت برعکس نیز انجام دهیم. یعنی متغیر را سمت راست نگه داریم و عدد را سمت چپ). بنابراین عدد −4 را که قرینۀ 4 است در دو طرف تساوی جمع میکنیم تا عدد 4 در سمت چپ از بین برود:
معادله به صورت زیر در میآید:
حالا دو طرف را در وارون ضریب x که همان 13 است ضرب میکنیم تا x تنها شود:
معادله به صورت ساده شدۀ زیر در میآید:
دیدید به چه سادگی و بدون سعی و خطا، پاسخ معادله را یافتیم. به طور کلی برای حل هر معادله باید معادله را تا جایی ساده کنیم که یک طرف تساوی، متغیر و طرف دیگر تساوی عدد باشد. در قمست بعدی از درسنامۀ معادله ریاضی هفتم ، مثالهای متنوعی از معادله حل خواهیم کرد تا کوچکترین مشکلی در این مبحث نداشته باشید.
مثالهایی از حل معادله ریاضی هفتم
مثال 1 معادله ریاضی هفتم: معادلۀ 2x−5=x را حل کنید.
بیشتر بخوانید: بهترین انیمیشن های سهگانه | 5 تا از بهترین ها را بشناسید
حل: سعی میکنیم معادله را طوری ساده کنیم تا در سمت چپ آن، متغیر باقی بماند و در سمت راست آن، عدد (البته همانطور که گفتیم میتوانید این کار را برعکس انجام دهید. یعنی متغیر را در سمت چپ و عدد را در سمت راست نگه داریم). با توجه به اینکه دنبال یافتن پاسخ معادله در مجموعۀ اعداد حقیقی هستیم، با متغیرِ این معادله نیز میتوانیم مانند یک عدد حقیقی رفتار کنیم. یعنی میتوانیم −x را با دو طرف تساوی جمع کنیم:
2x−5+(−x)=x+(−x)
⇒x−5=0
حال کافی است دو طرف معادله را با 5 جمع کنیم:
x−5+5=0+5
⇒x=5
به مثال بعدی از درسنامۀ معادله ریاضی هفتم دقت کنید.
مثال 2 معادله ریاضی هفتم: معادلۀ 4x+1=2x+3 را حل کنید.
حل: سعی میکنیم معادله را طوری ساده کنیم تا در سمت چپ آن، متغیر باقی بماند و در سمت راست آن، عدد (البته باز هم همانطور که گفتیم میتوانید این کار را برعکس انجام دهید. یعنی متغیر را در سمت چپ و عدد را در سمت راست نگه داریم). ابتدا −2x را با دو طرف تساوی جمع کنیم:
4x+1−2x=2x+3−2x
⇒2x+1=3
حال −1 را با دو طرف تساوی جمع میکنیم:
2x+1−1=3−1
⇒2x=2
در گام آخر، دو طرف تساوی را در 12 ضرب میکنیم:
2x×12=2×12
⇒x=1
مثالهایی دیگر از حل معادله ریاضی هفتم
مثال 3 معادله ریاضی هفتم: معادلۀ 3x−4=4x−3 را حل کنید.
حل: سعی میکنیم معادله را طوری ساده کنیم تا در سمت چپ آن، عدد باقی بماند و در سمت راست آن، متغیر (البته همانطور که گفتیم میتوانید این کار را برعکس انجام دهید. یعنی متغیر را در سمت چپ و عدد را در سمت راست نگه داریم). بنابراین، ابتدا −3x را با دو طرف تساوی جمع کنیم:
3x−4−3x=4x−3−3x
⇒−4=x−3
حال 3 را با دو طرف تساوی جمع میکنیم:
−4+3=x−3+3
⇒−1=x
به مثال بعدی از درسنامۀ معادله ریاضی هفتم دقت کنید.
مثال 4 معادله ریاضی هفتم: معادلۀ 2−3x=5x+1 را حل کنید.
حل: سعی میکنیم معادله را طوری ساده کنیم تا در سمت چپ آن، عدد باقی بماند و در سمت راست آن، متغیر (باز هم همانطور که گفتیم میتوانید این کار را برعکس انجام دهید. یعنی متغیر را در سمت چپ و عدد را در سمت راست نگه داریم). ابتدا 3x را با دو طرف تساوی جمع کنیم:
2−3x+3x=5x+1+3x
⇒2=8x+1
حال −1 را با دو طرف تساوی جمع میکنیم:
2−1=8x+1−1
⇒1=8x
در گام آخر، دو طرف تساوی را در 18 ضرب میکنیم:
1×18=8x×18
⇒18=x
زنگ آخر کلاس معادله ریاضی هفتم
همانطور که گفتیم، به یک تساوی که دو طرف آن عبارت جبری باشد، معادله میگوییم. دیدیم که برای یافتن پاسخ معادلات میتوان عبارات جبری یا اعداد را به دو طرف تساوی اضافه و یا در دو طرف تساوی ضرب کرد. در مثالهای مختلفی که حل کردیم، معادله را طوری ساده کردیم که یک طرف آن متغیر و طرف دیگر آن اعداد باشد. به این صورت توانستیم پاسخ معادلات را بیابیم.
تاریخچه
معادلات همراه با اعداد، از اولین دستاوردهای ریاضی بشرند. آنها در قدیمی ترین اسناد ریاضی، مکتوب، فی المثل، در متون میخی بابلیهای باستان، که به هزاره قبل از میلاد بر می گردند، و پاپیروسهای مصری باستان، که به امپراطوری میانه در حدود 1800 ق.م. بازگشت دارند، آمده اند.
بنا به ساختار جامعه بابلی مسائل مربوط به تقسیم ارث از اهمیت بسیاری برخوردار بودند. اولین پسر همواره بیشترین سهم را دریافت می کرد، دومی بیشتر از سومی، و به همین ترتیب.
در حالی که مسائل مطرح در بابل ،مجهول نسبتاً واضح توصیف شده است، در پاپیروس های مصری با علامت “h” نمایش داده شده است، که توده یا گردایه را نشان می دهد. چنین محاسباتی نسبتاً زیاد رخ می دهند و متناظر با معادلات خطی ما هستند. مقایسه ای بین متنی مصری از پاپیروس مسکو و نماد نویسی جدید این نکته را روشن می سازند.
پیش از این که زبان نمادین جبری مطرح شود، معادلات را بالاجبار با کلمات می نوشتند حتی فرانسواویت که معمولاً به ویتا موسوم است که شایستگی های بسیاری در زمینه جبر دارد از کلمه لاتین برای برابر بودن استفاده می کرد
علامت برابری = که امروزه متداول است توسط روبرت رکورد پزشک دربار سلطنتی مطرح شد، اما زمان قابل ملاحظه ای طول کشید تا این علامت مقبولیت عام یافت.
وی این طرح را در کتاب درسی جبری که به صورت گفتگو نوشته شده بود و عنوانش “the whetstone of witte” بود مطرح و انگیزه انتخاب ان را با گفتن مطالب زیر بیان کرد «در این مورد همان گونه که قالباً در عمل انجام می دهم یک جفت خط توامان می گذارند این چنین = = =, زیرا هیچ دو شیی نمی توانند برابر محض باشند.
با نوشته شدن کتاب جبر و مقابله توسط خوارزمی در سده های سوم و چهارم هجری، جبر وارد ریاضیات شد، و به حل معادله ها پرداخته شد.خود واژه جبر به معنای جبران کردن و مقابله به معنای روبه رو قرار دادن دو سوی برابری است.
مجموعه جواب
کار با مجموعه معینی از اعداد، موسوم به حوزه اصلی و مجموعه مشخصی از متغیرها که عناصری از حوزه اصلی با زیر مجموعه ای، موسوم به حوزه تغییرپذیری را می توان به جای آنها قرارداد، آغاز می شود.
در مشخص کردن حوزه اصلی و حوزه تغییر پذیری،N به جای مجموعه اعداد طبیعی، Z به جای مجموعه اعداد صحیح،Q به جای مجموعه اعداد گویا،R به جای مجموعه اعداد حقیقی و C به جای اعداد مختلط قرار می گیرد.
بیشتر بخوانید:
اینترنت رایگان شاد در سال تحصیلی جدید ادامه خواهد داشت / اعداد صحیح چیست؟ | به چه اعدادی صحیح گفته میشود / ضرب و تقسیم کسر ها | روش های آسان با حل تمرین / ضرب و قسیم اعداد مخلوط | آموزش آسان به همراه مثال / جمع و تفریق عدد های مخلوط | آموزش تصویری همراه با نحوه درست جمع و تفریق / فصل سوم کتاب ریاضی ششم (اعداد اعشاری) | تدریس و آموزش از روی کتاب /
ممنون که تا آخر این مطلب ما را همراهی کردید. اگر این نوشتار برای شما مفید بود حتما برای ما کامنت بگذارید. نظرات خود را درباره نوشتار معادله چیست با زنگ تفریح درمیان بگذارید.